К доказательству теоремы Пифагора

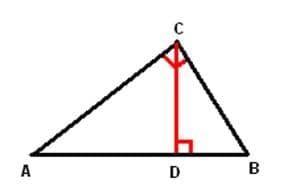
К доказательству теоремы Пифагора можно применить определение косинуса острого угла прямоугольного треугольника.

Доказательство:

По определению косинуса угла:

\( \cos A = {AD \over AC} = {AC \over AB} \),

Отсюда \( AB * AD = AC^2 \).

Аналогично,

\( \cos B = {BD \over BC} = {BC \over AB} \).

Отсюда \( AB * BD = BC^2 \).

Складывая полученные равенства почленно и замечая, что \( AD + DB = AB \), получим:

\( AC^2 + BC^2 = AB (AD + DB) = AB^2 \)

Доказательство закончено.